Your Diffusion Model is Secretly a Zero-Shot Classifier

Alexander C. Li     Mihir Prabhudesai     Shivam Duggal     Ellis Brown     Deepak Pathak

Carnegie Mellon University
ICCV 2023

"Diffusion Classifier"

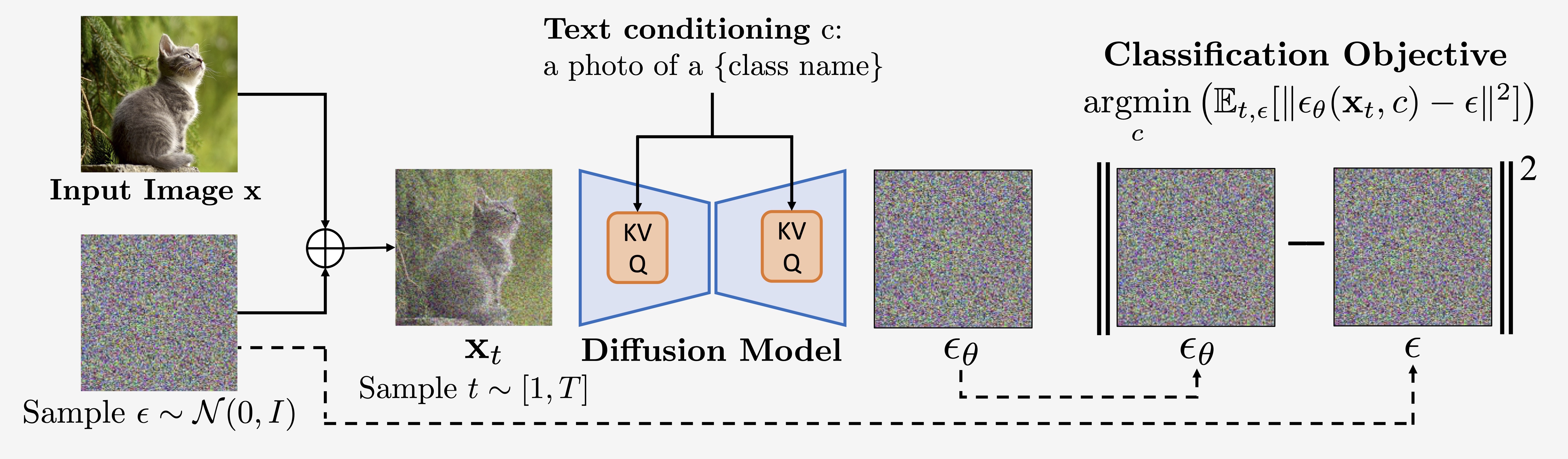
Diffusion Classifier method.

Given an input image \(\mathbf x \) and text conditioning \(\mathbf c\), we use a diffusion model to choose the class that best fits this image. Our approach, Diffusion Classifier, is theoretically motivated through the variational view of diffusion models and uses the ELBO to approximate \(\log p_{\theta}(\mathbf x|\mathbf c).\) Diffusion Classifier chooses the conditioning \(\mathbf c\) that best predicts the noise added to the input image. Diffusion Classifier can be used to extract a zero-shot classifier from a text-to-image model (like Stable Diffusion) and a standard classifier from a class-conditional model (like DiT) without any additional training.

Abstract

The recent wave of large-scale text-to-image diffusion models has dramatically increased our text-based image generation abilities. These models can generate realistic images for a staggering variety of prompts and exhibit impressive compositional generalization abilities. Almost all use cases thus far have solely focused on sampling; however, diffusion models can also provide conditional density estimates, which are useful for tasks beyond image generation. In this paper, we show that the density estimates from large-scale text-to-image diffusion models like Stable Diffusion can be leveraged to perform zero-shot classification without any additional training. Our generative approach to classification, which we call Diffusion Classifier, attains strong results on a variety of benchmarks and outperforms alternative methods of extracting knowledge from diffusion models. Although a gap remains between generative and discriminative approaches on zero-shot recognition tasks, our diffusion-based approach has significantly stronger multimodal compositional reasoning ability than competing discriminative approaches. Finally, we use Diffusion Classifier to extract standard classifiers from class-conditional diffusion models trained on ImageNet. Our models achieve strong classification performance using only weak augmentations and exhibit qualitatively better "effective robustness" to distribution shift. Overall, our results are a step toward using generative over discriminative models for downstream tasks.

Classification with diffusion models

In general, classification using a conditional generative model can be done by using Bayes' theorem on the model predictions and the prior \(p(\mathbf{c})\) over labels \(\{\mathbf{c}_i\}\):

\begin{equation} p_\theta(\mathbf{c}_i \mid \mathbf{x}) = \frac{p(\mathbf{c}_i)\ p_\theta(\mathbf{x} \mid \mathbf{c}_i)}{\sum_j p(\mathbf{c}_j)\ p_\theta(\mathbf{x} \mid \mathbf{c}_j)} \label{eq:bayes} \end{equation}

A uniform prior over \(\{\mathbf{c}_i\}\) (i.e., \(p(\mathbf{c}_i) = \frac{1}{N}\)) is natural and leads to all of the \(p(\mathbf{c})\) terms cancelling. For diffusion models, computing \(\log p_\theta(\mathbf{x}\mid \mathbf{c})\) is intractable, so we approximate it with the ELBO (see paper §3.1), from which we have dropped constant and weighting terms:

\begin{align} \text{ELBO} \approx - \mathbb{E}_{t, \epsilon}[\|\epsilon - \epsilon_\theta(\mathbf{x}_t, \mathbf{c}_i)\|^2] \label{eq:elbo} \end{align}

We plug the modified ELBO Eq. \ref{eq:elbo} into Eq. \ref{eq:bayes} to obtain the posterior over \(\{\mathbf{c}_i\}_{i=1}^N\):

\begin{align} p_\theta(\mathbf{c}_i \mid \mathbf{x}) &\approx \frac{\exp\{- \mathbb{E}_{t, \epsilon}[\|\epsilon - \epsilon_\theta(\mathbf{x}_t, \mathbf{c}_i)\|^2]\}}{\sum_j \exp\{- \mathbb{E}_{t, \epsilon}[\|\epsilon - \epsilon_\theta(\mathbf{x}_t, \mathbf{c}_j)\|^2]\}} \label{eq:posterior} \end{align}

We compute an unbiased Monte Carlo estimate of each expectation by sampling \(N\) \((t_i, \epsilon_i)\) pairs, with \(t_i \sim [1, 1000]\) and \(\epsilon \sim \mathcal{N}(0, I)\), and computing

\begin{align} \frac{1}{N}\sum_{i=1}^N \left\|\epsilon_i - \epsilon_\theta(\sqrt{\bar \alpha_{t_i}}\mathbf{x} + \sqrt{1-\bar\alpha_{t_i}} \epsilon_i, \mathbf{c}_j)\right\|^2 \label{eq:monte_carlo} \end{align}

By plugging Eq. \ref{eq:monte_carlo} into Eq. \ref{eq:posterior}, we can extract a classifier from any conditional diffusion model. This method, which we call Diffusion Classifier, is a powerful, hyperparameter-free approach that leverages pretrained diffusion models for classification without any additional training. Diffusion Classifier can be used to extract a zero-shot classifier from a text-to-image model like Stable Diffusion, to extract a standard classifier from a class-conditional diffusion model like DiT, and so on.

Zero-shot Classification

We build Diffusion Classifier on top of Stable Diffusion, a text-to-image latent diffusion model trained on a filtered subset of LAION-5B. Our zero-shot classification method is competitive with CLIP and significantly outperforms the zero-shot diffusion model baseline that trains a classifier on synthetic SD data. It also generally outperforms the baseline trained on Stable Diffusion features, especially on complex datasets like ImageNet. This is especially impressive since the "SD Features" baseline uses the entire training set to train a classifier.

Zero-shot classification performance on a suite of tasks.
Zero-shot? Food CIFAR10 FGVC Pets Flowers STL10 ImageNet ObjectNet
Synthetic SD Data ✓ 12.6 35.3    9.4 31.3 22.1 38.0 18.9    5.2
SD Features ✗ 73.0 84.0 35.2 75.9 70.0 87.2 56.6 10.2
Diffusion Classifier ✓ 77.7 88.5 26.4 87.3 66.3 95.4 61.4 43.4
CLIP ResNet50 ✓ 81.1 75.6 19.3 85.4 65.9 94.3 58.2 40.0
OpenCLIP ViT-H/14 ✓ 92.7 97.3 42.3 94.6 79.9 98.3 76.8 69.2

Compositional Reasoning

We compare our zero-shot Diffusion Classifier method to CLIP and OpenCLIP on Winoground, a popular benchmark for evaluating the visio-linguistic compositional reasoning abilities of vision-language models. This benchmark tests whether models can match captions to the correct images when certain entities are swapped in the captions.

Winoground examples
Results on selected Winoground image-caption pairs.

Diffusion Classifier significantly outperforms both contrastive baselines. Since Stable Diffusion uses the same text encoder as OpenCLIP ViT-H/14, this improvement must come from better cross-modal binding of concepts to images. Overall, we find it surprising that Stable Diffusion, trained with only sample generation in mind, can be repurposed into such a good classifier and reasoner.

Zero-shot reasoning results on Winoground
Model Object Relation Both Average
Random Chance 25.0 25.0 25.0 25.0
CLIP ViT-L/14 27.0 25.8 57.7 28.2
OpenCLIP ViT-H/14 39.0 26.6 57.7 33.0
Diffusion Classifier 46.1 29.2 80.8 38.5

Strong Standard Classification Ability

We use Diffusion Classifier to obtain a standard 1000-way classifier on ImageNet from a pretrained Diffusion Transformer (DiT) model. DiT is a class-conditional diffusion model trained solely on ImageNet-1k, with only random horizontal flips and no regularization. We compare Diffusion Classifier in this setting to strong discriminative classifiers like ResNet-101 and ViT-B/16 in the table below. We highlight cells in green where Diffusion Classifier outperforms.

Diffusion Classifier performs well ID and OOD.
Method ID OOD
IN IN-v2 IN-A ObjectNet
ResNet-18 70.3 57.3 1.1 27.2
ResNet-34 73.8 61.0 1.9 31.6
ResNet-50 76.7 63.2 0.0 36.4
ResNet-101 77.7 65.5 4.7 39.1
ViT-L/32 77.9 64.4 11.9 32.1
ViT-L/16 80.4 67.5 16.7 36.8
ViT-B/16 81.2 69.6 20.8 39.9
Diffusion Classifier (256x256) 77.5 64.6 20.0 32.1
Diffusion Classifier (512x512) 79.1 66.7 30.2 33.9

Diffusion Classifier achieves 79.1% top-1 accuracy on ImageNet, which is stronger than ResNet-101 and ViT-L/32. To the best of our knowledge, our approach is the first generative modeling approach to achieve ImageNet accuracy comparable with highly competitive discriminative classifiers. This is especially impressive since the discriminative models are trained with highly tuned learning rate schedules, augmentation strategies, and regularization.

Effective robustness on ImageNet-A
Diffusion Classifier exhibits "effective robustness," where it achieves much better OOD accuracy than expected based on its ID accuracy.

BibTeX

@InProceedings{li2023diffusion,
    author    = {Li, Alexander C. and Prabhudesai, Mihir and Duggal, Shivam and Brown, Ellis and Pathak, Deepak},
    title     = {Your Diffusion Model is Secretly a Zero-Shot Classifier},
    booktitle = {Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV)},
    month     = {October},
    year      = {2023},
    pages     = {2206-2217}
}